What does the “N” Mean Anyway? Living in a Metric World

Even data sheets and technical references meant for U.S. engineering audiences (for whom the English units of the Imperial Measurement System still reign supreme) detail forces in Newtons. This is in part because the rest of the world uses the metric system to which expressions of Newtons belong — also defined by the Système International of Units (SI) — and globalization has come to demand more universally applicable equipment. It’s also because expressions using Newtons abbreviated N are far more logical and far less confusing than those using Imperial expressions. 

In technical communications relating to linear-motion components (including those sold by Rollon) Newtons are used as the unit of measure for both: 

• The forces a motion system can generate. 
• The payloads that can be transported by a motion system. 

The unit of Newtons derive from the scientific trilogy known as the Philosophiæ Naturalis Principia Mathematica published by Sir Isaac Newton in 1687 to describe mathematics useful to the field of mechanics as well as basic laws of physics. Indispensable to the design of industrial machinery, the Principia first described the three universal laws of motion that define relationships between objects, forces, and resultant motion — including Newton’s second law of motion stating: 

F = m ⋅ a 

Where F = Force in the unit of Newtons; m = mass; and a = acceleration. Using typical metric units, mass is in kilograms or kg and acceleration in m/sec² — meters per second squared and 1 kg ⋅ m/sec² is one Newton (1 N) of force. 

One Newton (1 N) is the force needed to accelerate at 1 m/sec² a 1-kg mass. The unit is used in a vast array of motion system calculations. Image: Oliver Perez | Dreamstime 

The F = m ⋅ a equation is used to calculate force F needed to accelerate a given mass m of a payload riding a linear motion system or transported by a linear actuator. Converting between these values with this equation is quite common during the sizing and specification of linear motion designs. 

Check out this video for a full walkthrough of how to calculate and use actuator forces as well as forces and moment loads associated with workpieces and other transported items. 

F is also used to describe the weights of objects such as payloads. Here, acceleration is 9.81 m/sec² — that due to gravity on Earth. So, except for satellite, rover, and other applications in space, gravitational acceleration of a 1-kg mass makes for a force of 9.81 N. 

Comparing Newtons to other expressions of force 

In contrast with the expression of forces in Newtons (and metric expressions of mass) Imperial or English units are somewhat more complicated. However, there are machine designs for which motion components come with dimensions designed and expressed in metric as well as Imperial units. So, taking time to remember the difference between the two systems of units is useful. 

Imperial units include two different units of pounds — that for the weights of objects (sometimes designated in pounds-force or lbƒ) and that for the masses of objects (sometimes designated in slugs). Acceleration is expressed in ft/sec² and 1 lbƒ is the force needed to accelerate at 1 ft/sec² a mass of 1 slug. Entering these values into F = m ⋅ a and accounting for gravitational acceleration on Earth of about 32.2 ft/sec² yields: 

F = 1 slug ⋅ 32.2 ft/sec² = Weight (force exerted by 1 slug) = 32.2 lbƒ. 

In another organization of Imperial units called the English Engineering system, mass is in pounds-mass lbm and Newton’s second law includes a 32.2 lbm-ft/lbƒ-sec² gravitational constant for F = m ⋅ a ÷ gravitational constant. This rectifies the units of measure so that: 

F = lbm ⋅ ft/sec² ÷ lbm-ft/lbƒ-sec² = lbƒ. 

Typical designs (excluding those for satellites, rovers, and other applications in space) can be assumed to have an acceleration due to gravity on Earth, and the modified second law a = 32.2 ft/sec² so in fact a 1 lbm-mass under these typical conditions exerts a weight of 1 lbƒ. 

One Newton equals about 0.224809 lbƒ (and 1 lbƒ ≈ 4.448222 N) but it’s important to verify any expressions in pounds are in fact related to some force and not a mass. 

Newtons in expressions of linear-motion moment capacities 

For linear-motion applications, Newtons are used to express both static and dynamic load capacities as detailed in this Rollon blog entry: Differences Between Static and Dynamic Load Ratings. Newtons are also used in expressions of moment loading on mechanical components … and in fact, these types of loading are especially important to consider when specifying and sizing linear guides and linear actuators. Moment loads — expressed as Newton-meters or Nm — are forces applied at some distance from an axis that (if unopposed or unresolved) would spur some deflection or rotation. 

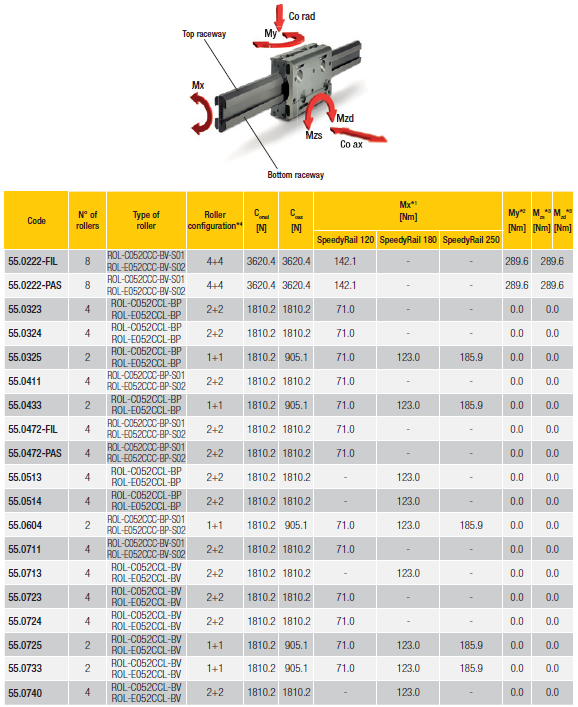
Shown here is a small sample of load (C₀ expressed in Newtons) and moment (M_x , M_y , M_zs , and M_zd in Newton-meters or Nm) capacities for Rollon Speedy Rail self-supporting linear guides. 

A moment load that would otherwise induce up and downward movements (traditionally around the Y axis) is called pitch; right and left movements (traditionally around the Z axis) called yaw; and rotational movements (traditionally around the X axis) called roll. 

Connect with Rollon to define design requirements 

For more information on the force capabilities of various linear actuators from Rollon, visit rollon.com. Or identify viable design solutions by entering your own application’s parameters into Rollon’s Product Selector Tool, myRollon. Through the myRollon site, engineers can also connect with Rollon experts to help solve challenging payload requirements.